L'arbre, un modèle fractale ?

Peut on considérer qu’un arbre soit issu d’un modèle fractal ?

Étude de cas sur des sapins de Nordmann

a) Mesures concrètes

Nous avons mesuré 5 sapins. Cependant, deux d'entre eux présentaient des malformations. Parmi ces 5 cas, nous n'en avons gardé que 3 qui semblaient intéressants par leur régularité.
Sapin n°1 :

1. Nombre d'étages de branches: 6
2. Nombre de branches par étage : 5
3. Nombre de branches après 2 itérations : 3
4. Angle mesuré entre chaque branche : 72°
5. Angle mesuré tronc/branche : 100°
6. Longueur de branche tronc/ramification suivante : 12cm
7. Rapport de longueur dès la seconde itération (longueur première branche / longueur totale) : 2/5
8. Haut du sapin : 5 ramifications
9. Bas du sapin : 14 ramifications

Sapin n°2 :

1. Nombre d'étages de branches: 8
2. Nombre de branches par étage : 6
3. Nombre de branches après 2 itérations : 3
4. Angle mesuré entre chaque branche : 60°
5. Angle mesuré tronc/branche : 100°
6. Longueur de branche tronc/ramification suivante : 14cm
7. Rapport de longueur dès la seconde itération (longueur première branche / longueur totale) : 2/5
8. Haut du sapin : 6 ramifications
9. Bas du sapin : 14 ramifications

Sapin n°3 :

1. Nombre d'étages de branches: 6
2. Nombre de branches par étage : 6
3. Nombre de branches après 2 itérations : 3
4. Angle mesuré entre chaque branche : 60°
5. Angle mesuré tronc/branche : 110°
6. Longueur de branche tronc/ramification suivante : 13cm
7. Rapport de longueur dès la seconde itération (longueur première branche / longueur totale) : 1/3
8. Haut du sapin : 5 ramifications
9. Bas du sapin : 12 ramifications

On peut constater que sur chaque sapin, l'angle à chaque itération est sensiblement le même que celui mesuré entre chaque branche d'un étage. De plus, on trouve le même nombre de bourgeons axillaires qu'il y a de ramification, sur les extrémités de chaque branche. Il faut par contre noter que des 5 ou des 6 bourgeons, il n'y en a que 3 qui poussent. Cette particularité semble être due au manque de lumière de certains des bourgeons, en effet, les bourgeons les plus développés montrent 3 bourgeons principaux, et 2 ou 3 autres plus petits toujours logés en dessous des trois autres, car c'est ici qu'il y a le moins de lumière.

b) Conjecture

Chaque sapin possède un algorithme de définition fractale qui lui est propre et qui s'applique de manière presque parfaitement exact sur l'ensemble des branches. Cependant, des facteurs externes peuvent influer sur cette définition et fausser la régularité acquise, comme par exemple le vent (anémomorphose), des animaux qui se nourrissent des bourgeons et des jeunes pousses, ou encore l'absence de lumière qui provoque un dérèglement des rapports.

c) Simulation

Le programme utilisé ci-dessous est téléchargeable ici

Algorithme

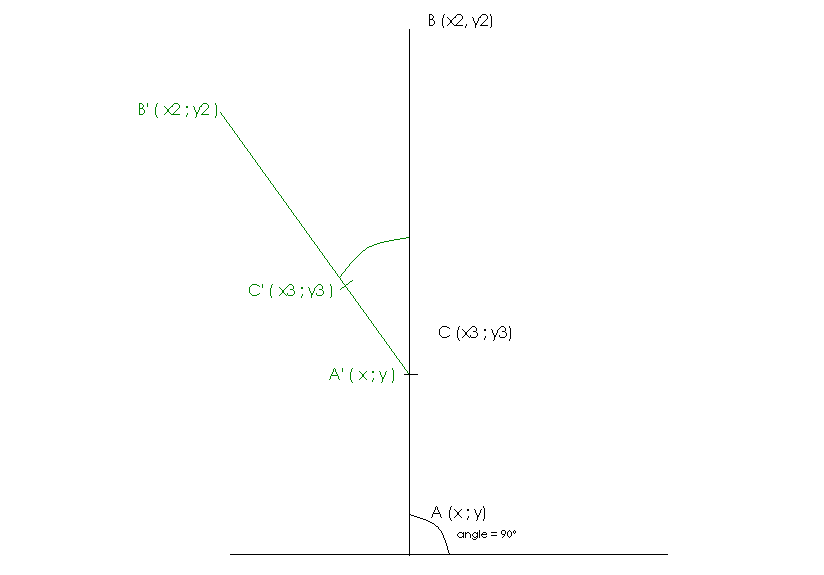
Pour simuler un arbre fractal, nous avons créé un algorithme en C++ (langage de programmation). Soit k le rapport de longueur, α l'angle branche mère / branche fille, A, B, et C trois points du plan. Voici l'algorithme :

1. On passe à l'algorithme x et y, l'angle de la branche fille, la longueur de la branche fille
2. Soit un point A(x ; y)
3. Soit un point B(x₂ ; y₂)
   x₂ = longueur * cos (angle) + x
   y₂ = longueur * sin (angle) + y
4. On trace [AB]
5. On recherche C(x₃ et y₃) appartennant à [AB], selon le rapport d'homothétie choisi dans les paramètres du programme
6. On se place en C, et on trace trois branches
   On revient à l'étape 1, on prend x> = x₃ et y = y₃, on incrémente l'angle de α°, on passe longueur_{branche fille} = k * longueur_{branche mère} => C'est la branche de gauche
   On revient à l'étape 1, on prend x = x₃ et y = y₃, on garde α°, on passe longueur_{branche fille} = longueur_{branche mère} => C'est la branche du milieu
   On revient à l'étape 1, on prend x = x₃ et y = y₃, on incrémente l'angle de -α°, on passe longueur_{branche fille} = k * longueur_{branche mère} = >C'est la branche de droite

Résultats

Nous avons dans chacun des cas utilisé les paramètres étudiés sur les 3 sapins. L'image ainsi produite présente un sapin vu d'en haut, composé de trois couches. Les branches claires sont celles situées au sommet. Les branches sombre sont proches du sol.

Ici, l'interprétation n'est pas aisée, en effet, la multitude de branche ne permet pas de dissocier correctement chacune d'entre-elles. On remarque cependant à la périphérie que la forme semble hexagonale. Lors de nos analyses, nous avions en effet déjà noté cette particularité.

Même constat que pour la sapin 1

Ici, l'étude semble plus interessante. En effet, la forme générale du sapin est bien plus claire. Si nous comparons à de vrais sapins, il est notable que l'on peut trouver nombre de ressemblances (Exemple ici ou encore ici

Nous avons ensuite pris une photo d'une branche d'un sapin, et nous avons tenté de trouver l'algorithme correspondant. C'est ainsi que nous avons obtenu l'animation suivante.

d) Avantages

Disposant d'une structure 3D,  le sapin a un volume assez minimal et une surface très grande ce qui lui permet de réduire les dépenses énergétiques tout en maximisant les surfaces d'échanges. La respiration et la photosynthèse se servent de ces propriétés.

Page générée en -801ms. Code source libre