L'arbre, un modèle fractale ?

Peut on considérer qu’un arbre soit issu d’un modèle fractal ?

I. Définition : mathématique, simplifiée :

a) Définition simplifiée

Un objet est dit fractal, si d'une part, il apparaît comme irrégulier et fragmenté, et si d'autre part, ces irrégularités se conservent quand on observe un détail de l'objet.

Autrement dit, on peut reconnaître un objet fractal s'il a une forme plus ou moins fragmentée, et si on retrouve cette forme en changeant d'échelle.

b) Définition mathématique

À partir de 1970, Benoît Mandelbrot développe grâce aux ordinateurs une étude plus systématique de ces formes complexes, qu'il désigne d'un nouveau nom: les «fractales». Ce mot, qui se rapproche de «fractionné», «fragmenté», «fracturé», est à relier à une notion élémentaire et importante: l'homothétie interne, qui fournit un outil simple pour construire ces objets, étudier leur degré de complexité et déboucher sur la notion de dimension non entière, ou fractale.

On nomme fractale, une courbe ou surface de forme irrégulière ou morcelée qui se crée en suivant des règles déterministes ou stochastiques impliquant une homothétie interne.
Il est clair que cette définition n'est pas très précise, en effet, une fractale peut adopter une infinité de formes. De ce fait, pour déterminer qu'une figure soit fractale, on vérifie qu'elle réponde à certaines conditions, qui se trouvent aussi être des propriétés. Dans la partie suivante, nous vérifierons que les arbres vérifient les conditions citées.

c) Propriétés

Il est possible de faire une liste non exhaustive des ces propriétés.

Tout d’abord, ils suivent une homothétie interne, à laquelle on peut faire suivre, ou non, une rotation. Cela induit qu'une fractale a une surface limitée. C'est pourquoi, dans l'immense majorité des cas, le rapport de l’homothétie est inférieur à 1. De même, cette propriété induit le principe de récursivité interne, qui sera plus détaillée dans les exemples qui suivront. Ainsi, une fractale observée à une échelle 1:100 000 est ressemblante à cette même fractale à échelle 1 :10 si c'est une fractale stochastique, si c'est une fractale déterministe, les deux observations sont strictement les mêmes.

Ensuite, une fractale pure est créé par un nombre infini d’itérations. Les fractales se dessinent en fait en suivant des algorithmes de complexité variable. Chaque répétition de cet algorithme est appelée itération. Pour qu’une fractale soit mathématiquement parfaite, il faut que son algorithme ait été répété à l’infini, ce qui n'est pas réalisable, que ce soit à l’aide d’ordinateurs, ou dans la nature, où c’est la taille dees particules qui déterminent une limite minimale. Les algorithmes eux-mêmes répondent à des règles stochastiques (aléatoires), ou déterministes, ce qui fait que l’apparence de ceux-ci peut-être très variée. Dans notre, TPE, nous étudierons des fractales déterministes, c'est-à-dire que tous les paramètres sont fixés, et qu'ainsi il n'y a absolument pas d'aléatoire
De plus, dans le cas de la représentation d’une fractale dans un plan 2D, le périmètre de ce dernier est … infini ! Tandis que son aire tend vers une valeur fixe non nulle. Si la fractale est présentée dans un espace en 3D, son aire devient infinie, tandis que son volume est fini !

Enfin, une fractale a des dimensions non entières. Cependant, on représente toujours les fractales dans des dimensions entières. Cette notion, assez délicate à comprendre est facilement abordable grâce à des exemples. Ainsi, un point a pour dimension 0, une droite à pour dimension 1, un carré a deux dimensions, tandis qu’un cube est en 3 dimensions. Cependant, une fractale comme le flocon de Koch n’est pas une droite, donc pas en 1 seule dimension, mais ce n’est pas non plus un plan en 2 dimensions. La dimension non entière, appelée dimension de Hausdorff est déterminée par la formule n = s^d, où n est le nombre de morceaux, et s le rapport d’homothétie (ou la diminution que subit la fractale). La fonction logarithme permet de retrouver d = (log n) / (log s).
Attention, il est facile de confondre surface et dimension ! En effet, une fractale (en 2D) a une surface finie !

La côte bretonne. Sa dimension est estimée à 1.24.

d) Quelques exemples

Flocon de Koch

Si nous poursuivions les itérations, nous obtiendrons bien les 3 premières propriétés. Le triangle de Sierpinski présente à chauqe itération 3 représentations de lui même, donc n = 3, chacune étant réduite de facteur 2, s = 2. La dimension de Hausdorff est donc de log(3) / log(2) = 1.5849625. Cet exemple permet de se rendre compte qu'un objet fractal en 2 dimensions possède un périmètre infini (chaque itération l'augmentant), et une surface finie, tandis qu'un objet en 3D possède un volume fini, mais une surface infinie.
L'image ci-contre permet de comprendre le fonctionnement d'une fractale : on commence par tracer une suite de segment, puis, on remplace chacun des segments par la suite précédente. Ici, nous avons à chaque passage, ou itération, un segment supplémentaire.

Triangle de Sierpinski :

Ici, pour tracer le triangle, il faut tracer tracer 4triangles, et enlever celui du milieu. Chaque triangle fils (c'est-à-dire les triangles néoformés) est 3 fois plus petit que le triangle mère (c'est-à-dire celui qui le contient).
Donc, n = 4, s = 3, d = 1.26185951

Tapis de Sierpinski :

Ici encore, le calcul de la dimension n'est pas très dur. A chaque itération nous avons 8 carrés, chacun réduit de facteur 3.Le tapis de Sierpinski a donc pour dimension log(8)/log(3) = 1.89278926

Ensemble de Julia

Cette fractale est un petit peu plus complexe que les précédentes. En effet, le plan dans lequel elle est représenté est un plan complexe. Pour construire cette fractale, il faut utiliser une suite complexe de la forme z_n+1 = z_n² + c .
Pour construire cette fractale, il faut donc créer un simple algorithme qui placera les différents points de la suite complexe dans le plan complexe. La plupart des ensembles de Julia sont représentés avec des couleurs, elles dependent de combien d'itérations ont déjà été faites (la couleur change à chaque itération)

D'autres exemples :

d (val. approchée)	Nom	Remarques
1.2	Ensemble de Julia	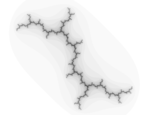Ensemble de Julia pour c=i
1,26	Attracteur de Hénon	La carte de Hénon canonique (a = 1,4 et b = 0.3) possède δ = 1,261 ± 0,003. Différents paramètres conduisent à différentes valeurs de δ
1,2619	Frontière de la Courbe Terdragon,	L-System : similaire à la courbe du dragon avec un angle de 30°. Le Fudgeflake est construit en juxtaposant 3 segments initiaux en triangle.
1,2619	Carré de Cantor	Ensemble de Cantor en deux dimensions.
1,2683	Ensemble de Julia pour z²-1	Ensemble de Julia pour c=-1.
1.3934	Lapin de Douady	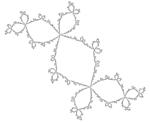Ensemble de Julia pour c=-0,123+0.745i.
1,4649	Fractale de Vicsek	Construit en substituant itérativement chaque carré par une croix de 5 carrés.
1,5000	>Courbe de Koch quadratique (type 2)	Appelée également « saucisse de Minkowski ».
1,5850	Arbre à trois branches	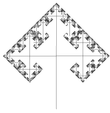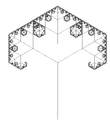Chaque branche porte trois branches (ici 90° et 60°). La dimension fractale de l'arbre est celle des branches terminales.
1,5850	Courbe de Sierpiński en pointe de flèche	Même limite que le triangle de Sierpiński (ci-dessus), mais obtenue par itérations d'une courbe unidimensionnelle.
1,6309	Triangle de Pascal modulo 3	D'une manière générale pour un triangle modulo k, si k est premier, la dimension fractale est 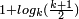$\scriptstyle 1 + log_k(\frac{k+1}{2})$
1,7712	Flocon hexagonal	Construit en substituant itérativement chaque hexagone par un flocon de 7 hexagones. Sa frontière est le flocon de Koch. Contient une infinité de flocons de Koch (en positif comme en négatif).
1,8617	Flocon pentagonal	Construit en substituant itérativement chaque pentagone par un flocon de 6 pentagones. Ici, $φ$ est le nombre d'or et vaut $\scriptstyle\frac{1+\sqrt{5}}{2}$
1,8928	Cube de Cantor	Ensemble de Cantor en trois dimensions.

Introduction - Etude de cas